一、前言
信堅近十年來修行，首在由定開慧，有智慧就能解決一切問題。有智慧就能深入信解一真法界，諸法實相。解悟了諸法實相，就知萬法唯心，一切法唯心所現，唯識所變。就知萬物一體，就能一以貫之。一經通，一切經通，一法通，一切法通。

因此，四年來，信堅對一乘佛經義理，有所解悟之後，就以此更深廣信解，首先回頭，快速看完老莊，再看四書五經。近幾個月來，又再以此諸法實相，萬法一體的觀點，回首重看信堅本行，高能物理，統一場論，超弦理論，量子力學，相對論，天文物理，宇宙論。因此張貼了三篇有關時間、及最新的宇宙膨脹模型的科普文章。有時間也會再張貼一篇全息宇宙論。

修行至一段落後，法法都是修行法門。近幾個禮拜，因孫子 紘燁先生 因緣，又回首重溫舊夢，以新見解認知，重解一些小學至高中的數學問題。此文是收集一些有趣數學問題，加上解題的思維方法。問題分小學、初中、高中程度，由易入難。

解答數學問題，可訓練多方面思維觀察的能力。最主要的挑戰是對於每題，你能找出幾種解法，同時也能找出最簡單的解法，及一般定律，才是高手。

二、小學班問題

【問題1】四個孩子
有四個孩子，恰好一個比另一個大一歲，他們的年齡相乘等於3024。算一算這四個孩子的年齡是多少？

1a. 分解法
3024 = 2x2x2x2x3x3x3x7 = 6x7x8x9
[要將3024分解成四分，最好的方法是找出最小乘數。7 給於解此問題重要提示。]

1b. 列表方法
1234    2345   3456    4567     5678     6789
  24        120     360     840      1680     3024

1c. 最簡單的一般解法是:
(3024)^1/4 =7.4  => 因此第二個孩子是 7 歲. 所以答案是 6, 7, 8, 9.

1d. 一般公式
如果有 n 個相連的正整數，其乘積是 N, 則此數列的第 [n/2] 數字是 [N^1/n]。 
( 註: [n/2],  [N^1/n]  的定義是 n/2, N^1/n 的整數值)。

譬如，
n=4, N=43680, 則 [N^1/4]=[14.46]=14. 因此, [n/2]=2, 答案是 13, 14, 15, 16.
n=5, N=1028160，則 [N^1/5] = [14.93] = 14. 因此, [n/2] = [2.5] = 2,
此五位數是 13, 14, 15, 16, 17.
n=7, N=1663200，則 [N^1/7] = [7.74] = 7. 因此, [n/2] = [3.5] = 3
此七位數是 5, 6, 7, 8, 9, 10, 11.
n=9, N=79833600，則 [N^1/9] = [7.55] = 7. 因此, [n/2] = [4.5] = 4,
此九位數是 4, 5, 6, 7, 8, 9, 10, 11, 12.

【問題2】21桶油的分法
供銷社運來21桶油。其中7桶是滿的，7桶是半桶， 還有7桶是空的。請問如何將它們分成三等分?

解題重點提示在於3, 7, 21 之間關聯: 21 = 3 x 7, or 3 = 21/7.
總共 7×2+7+0 = 21半桶. (全桶是兩個半桶) => 每個代銷商分七個半桶油
[答案是: 二滿桶三半桶二空桶，二滿桶三半桶二空桶，及三滿桶一半桶三空桶。]

滿桶               2    2     3
半桶               3    3     1
空桶               2    2     3
_______________________
總共半桶數    7    7     7

【問題3】孫子問題
(原文) : 今有物不知其數, 三三數之剩二, 五五 數之剩三, 七七數之剩二, 問物幾何? (白話翻譯): 有一堆東西, 不知道有幾個，如果三個三個去數, 剩餘二個; 五個五個去數, 剩餘三個; 七個七個去數, 剩餘二個; 問此物的總共數目是多少?

3a. 列表解法:
n            1    2    3     4     5     6     7     8     9
3n+2      5    8   11  14   17   20   23   26   29
5n+3      8   13  18   23  28   26
7n+2      9   16   23   30  37
答案有無限多: 105n+23 = 23, 128, 233, 338, 443, 547 …. , n 是正整數。

3b. 另一古代算經算法: 解此種問題的一般公式是
N = 3x5x7 n + A, where A = 3x5a +5x7b+3x7c = 15×2+35+21×3 = 128
A÷7 餘 2 => a =2
A÷3 餘 2 => b= 1
A÷5餘 3 => c= 3
因此，A = 105n + 128 > 0 都是答案 。 最小值是 23, (when n = -1).

3c. 其實，這解法也太複雜了，另一個最簡單的解法是:
A = 3x7n+2 滿足33數與 77數的條件。當n=1時，A= 23 也同時滿足55數的條件。因此 答案是 105n+23, 如3a.

3d.一般解法
有一堆東西, 不知道有幾個 N，如果3個去數, 剩餘 k₁ 個; 5個去數, 剩餘 k₂ 個; 7個去數, 剩餘 k₃ 個; 問此物的總共數目是多少?

N = 3x5x7n+A = 105n+A,
A=3x5a+5x7b+3x7c= (14+1)a +(36-1)b +(20+1)c
==>  a=k₃ , b=-k₁, c=k₂ 
==>答案是  N=105n+A， A=15k₃ -35 k₁ + 21k₂

例子:
此題，k₁=2, k₂=3, k₃=2, ==> A = 23
==> N = 105n + 23 = 23,128,233, 338, 443 …

若 k₁=2, k₂= 3, k₃=4, ==> A = 53
==> N = 105n + 53 = 53,158,263, 368, 473 …

若 k₁=1, k₂=3, k₃= 1   ==> A = 43
==> N = 105n + 43 = 43,148,253, 358, 463 …

【問題4】韓信點兵
每8人一隊或7人一隊都餘1人, 每5人一隊餘2, 已知兵員略多於兩千人, 問: 韓信有多少兵員?

4a. 列表解法
n              1    2    3     4     5     6    7     8     9    10   11   12   13 
x=5n+2    7  12  17    22  27   32   37   42   47   52   57   62   67 
x=7n+1    8  15   22   29  36   43   50    57  64
x=8n+1    9  17   25   33  41   49   57    65
5x7x8=280 ==> 一般的答案是 280n +57.
若 280n+ 57 > 2000 ==> 最小的n 是 7，總兵員是 280×7 + 57 = 2017.

4b. 算經解法:
總兵員是280n+A,
where A = 8x5xa + 5x7xb + 7x8xc = 7x8x2+ 8x5x3 + 5x7x3 = 337
由除以８餘１，得ａ＝３.除以７餘１，得ｂ＝３. 除以５餘２，得ｃ＝２.
280n+337 > 2000 ==> n = 6，總兵員是280n+A = 280 x 6 + 337 = 2017
[For n=-1， smallest number is -280+337 = 57.]

4c.最簡單解法
A = 8x7n+1 滿足88數與 77數的條件。當 n=1時， A=57 也同時也滿足55數的條件。再如4a, 280n+ 57 > 2000 ==> 最小的n 是 7，總兵員是 280×7 + 57 = 2017.

4d. 一般解法
韓信總兵員N 最接近 2000，88數剩 k₁, 77數剩 k₂, 55數剩k₃, 問韓信總兵員N是多少?
N = 8x7x5n+A,  A = 8x5xa + 5x7xb +7x8xc
8x5xa =35a+5a =7m₁+k₂, 5a=k₂+7p₁ => p₁=-3k₂, 2k₂
=> a= -4k₂, 3k₂
5x7xb =32b+3b= 8m₂+k₁, 3b=k₁+8p₂=> p₂= -2k₁,k₁
=> b = -5k₁, 3k₁
8x7xc = 55c+c =5m₃+k₃, c=k₃+5p₃ => p₃= –k₃,0,k₃=>
c= -4k₃, k₃, 6k₃,
==> A = -160k₂+105k₁+56k₃

舉例:
k₁=1, k₂,k₃=1 => A=281, N=280n+281=1,281,561,841,1121,1401,1681,1961,2241
k₁=1,k₂, k₃=2 => A=57, N=280n+337=57,337,617,1457,1737,2017
k₁=3, k₂,k₃=3 => A=163, N=280n+163=163,443,723,1283,1563,1843,2123

【問題5】: 那一號隊員最後離開
1-50號運動員按順序站一排，「一、二」報數，隊長讓報單數的運動員離開隊伍。剩下的隊員再重新報數，新的單數又離開了隊伍。請問，哪號運動員最後離開？

5a. 列表法:
第一次剩: 2, 4, 6 … 48, 50 (2的倍數)
第二次剩: 4, 8 , 12, … 44, 48 (4的倍數)
第三次剩: 8, 16, 24, … 40, 48 (8的倍數)
第四次剩: 16, 32, 48 (16的倍數)
第五次剩: 32 (答案)

5b.代數法
答案是 2ⁿ, 滿足 2ⁿ <50 的最大數目 ==>  n=5, 2⁵= 32.
[信堅註: 上題如改成: 有 1000 運動員排成一列，那號運動員最後離開?
答案是 2⁹ = 512.]

【問題6】黑白棋子數目
有黑白棋子一堆，黑子是白子的2倍，現在從堆內每次取出黑子4個，白子3個，等到幾次後，白子已盡而黑子還餘16個，求黑白棋子各多少？

6a. 列表解法
假設要抽 n 次，則黑子總數目是 4n+ 16，白子總數目是 3n
抽的次數   n     1    2    3     4     5     6     7      8
White       3n    3    6    9   12   15   18   21    24
Black 4n+16   20  24  28  32   36   40   44    48

6b.代數解法
4n+16 = 2x3n ==> n=8. 因此黑子數目= 4×8+16= 48, 白子數目= 3×8= 24.]

【問題7】幾本書
小紅、小虎、小芳和小華４個孩子共有 45本書，但是不知道每人各有幾本。如果變動一下：小紅的減２本，小虎的加２本，小芳的增加一倍，小華的減少一半，那麼４個是個孩子的書本就一樣多。請你算一算，每個孩子各有幾本書？

7a. 代數解法
假設 小紅有 X 本書，則 X-2 = 小虎+2 = 2小芳 = 小華/2
==> 小虎 =X-4,   小芳= (X-2)/2,    小華=2(X-2)
四人的總和  45= X + (X-4) +(X-2)/2 +2(X-2) = 9X/2 – 9 ==> X = 12

7b. 列表解法 [書的數目必須是偶數 (由小華能減一半看出)]
小紅      6     8    10    12
小虎      2     4     6      8
小芳      2     3     4      5
小華      8    12  16     20
_________________________
Total   18    27   36    45   (以9的倍數增加)

二、 初中班問題

【問題8】一道六位數問題
這是一道很古老的算術問題：有一個 六位數的正整數abcxyz，乘以6之後，變成xyzabc. 問: 這六位數是什麼？

關鍵在於將六位數分成 abc 及 xyz 兩組。
6abcxyz =6000abc+6xyz
=xyzabc = 1000xyz+abc => 5999abc = 994xyz

除以7 得=> 857 abc = 142 xyz
因142 及 857 是不可再分的 質數， 所以 abc = 142, xyz = 857
即這六位數正整數abcxyz是142857。
[註: 三位數abc 符號的定義是: abc =100a + 10b +c.]

【問題9】兄弟兩人年齡
今年兄弟兩人的歲數加起來是55歲，曾經有一年，哥哥的歲數是弟弟今年的歲數，那時哥哥的歲數恰好是弟弟的兩倍，請問兄弟今年的年齡各是多少？

假設哥哥的歲數=X，弟弟的歲數=Y，在A年前。則依題可得下面三個方乘式:
X+Y=55,
X-A=Y,
X-A=2(Y-A).
將第二公式Y=X-A 代入第三公式，即得 X=3A.
將X=3A代入第二公式，即得 Y=2A.
將此 X,Y帶入第一公式即得 A=11. 因此，X=33, Y=22.
答案是: 哥哥33歲, 弟弟22歲。

【問題10】赴宴的人數
大廳裡正舉行宴會，每人端起酒杯都要跟其他所有的人碰一次杯，一共碰杯136次，你能說出有多少人參加宴會嗎？

10a. 代數解法
假設有X人來參加宴會。
第一個人要碰X-1次，
第二個人要碰X-2次，
第三個人要碰X-3次，
………………..
第（X-1），只要碰1次，
第X个就不用再碰了。
因此總共是: (X-1)+(X-2)+(X-3)+……+3+2+1=136
==> X (X-1)/2 = 136
==> X² – X – 272 = 0，
解得 X= [1+(1+1088)]^1/2/2 = (1+33)/2 = 17.  (X是正整數)

[註: 利用數學公式: 1+2+3+ …+x = (x+1)x/2, 及 二次方程式 ax²+bx+c=0 的一般解答是:

這些公式是要背熟的。]

10b. 另法解 X(X-1)/2 = 136 = 碰杯數
X² – X – 272 = 0 ==> X = (X+272)^1/2 > 272^1/2 = 16.49 (X>0 的正整數)
因 X > 16. 從 X = 17 算起:  當 X=17 時，碰杯數 = 17×16/2 = 136 剛好是答案。

10c. 一般公式
如果有 X 人參加宴會， 碰了 N 次杯， 則公式是 X² – X – 2N = 0.
==> X > (2N)^1/2
譬如總共碰了 N=528次，則 X > 32.50 ==>   X = 33 是答案。
譬如總共碰了 N=171次，則 X > 18.49 ==>   X = 19 是答案。

【問題11】植樹問題
有九株樹，要栽十行，每行三株，共有三種解法，請你幫忙想一想。(例如：田字型有八行。)
解答如下圖:

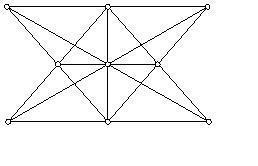
【問題12】速算問題
如果已知:
12345679× 9 = 111111111
12345679×18 = 222222222
12345679×36 = 444444444
你能快速猜出下面問題的答案嗎?
12345679×54=?
12345679×81=?
[暗示: 18 =2×9, 36 =4×9, 54 =6×9, 81=9×9]

【問題13】四位數abcd = (a+b+c+d)⁴ , 試問此四位數為何?
解答的關鍵在於四位數目，1000 < abcd = (a+b+c+d)⁴ < 9999 => 四方根是  5.62 < a+b+c+d < 10，限定了求解的範圍。
a+b+c+d          6          7         8           9
(a+b+c+d)⁴    1296   2401   4096      6561
(a+b+c+d)’     18          7        19         18

【問題14】訂購教科書
校長問：「這學期訂購的教科書都送來了嗎？」 老師：「按計畫是分三次送來，第一次是303本，第二次是五分之一，都送到了。當還有七分之Ｘ沒送到。」 校長：「Ｘ是多少？」老師：「Ｘ是整數，請您算一算。」 請大家來算一算Ｘ是多少？同時也算一下訂購了多少本書 N？

N=303+ N/5 +XN/7 => 35N = 35×303 + (7+5X) N
=> (28-5X) N = 3x35x101
因 3, 35, 101 都是質數, X是大於零的整數 ==> 28 – 5X = 3
==> 唯一解是 X= 5, N=35×101 =3535.

【問題15】四位數abcd = (a+b+c+d)³ 試問此四位數為何?
解答: 因 1000< abcd= (a+b+c+d)³ < 9999, => 10 < a+b+c+d < 21.54 a+b+c+d       11     12     13    14      15      16     17    18     19     20
(a+b+c+d)³ 1331 1728 2197 2744  3375 4096 4913 5832 6859  8000 
(a+b+c+d)’      8      18     19    17      18     19     17     18     28       8
答案是 4913 或 5832.

【問題16】分牛奶的難題
十八世紀法國著名數學家巴遜，據說他最初的願望不是搞數學，他的父母原希望他做個醫生，噹是由於一個偶然的機會，才使他改變了志願。 有一次，巴遜跟他的朋友到鄉間去旅行。有兩個路人到他的住處附近購買牛奶。主人從地窖裡拿來了一桶八公斤的牛奶，買者請求對半分。使主人感到為難的是：他身邊沒有磅秤，只有兩個瓦罐，大的可以裝五公斤，小的裝三公斤，怎麼辦呢？巴遜想了一下，便自告奮勇地為主人解決了這個難題。他的朋友邦稱贊他有數學天才，一致鼓勵他攻讀數學，巴遜接受了朋友的忠告，刻苦勤奮地埋頭攻讀數學，後來果然成為法國赫赫有名的數學家。 這個問題並不太複雜，只要肯動腦筋，一定可以解決的。你願試一試嗎？

列表解答:
8公斤桶|    8   3   3   6   6   1   1   4
5公斤桶|    0   5   2   2   0   5   4   4  
3公斤桶|    0   0   3   0   2   2   3   0

三、高中班問題

【問題17】數字編組
這裏有十個數字：21、22、34、39、44、45、65、76、133、153。請你把它編成兩組，每組５個數，並且兩組數目的乘積會相等。

這10 個數字相乘後的平方根 (square root) 是 349,188,840. 它是 5 個數目的乘積。

在此兵分兩路:
==>133×2625480= (133x34x45)x 1716==> 133x45x34x(39×44) 
[註: 2625480不能被21, 76, 153 除]
==> 153×2282280=(153x21x76)x1430 ==> 153x21x76x (22×65) 
[註: 2282280 不能被34, 45, 133 除]
因此，答案是 (34,39,44,45,133) 及 (21,22,65,76,153) 兩組。

【問題18】分糖
春節的時候媽媽給小龍買了一斤水果糖（不超過100顆）。上午小龍吃了一塊，然後把剩下的糖分出三分之一送給奶奶。下午小龍又吃了一塊，再把剩下的他分出三分之一送給隔壁的小弟弟。晚上小龍又吃了一塊，然後把剩下的糖再分出三分之一給爸爸媽媽吃。第二天，來了三位小朋友，小龍把剩下的糖果分成三份，最後還多了一個。請你算一算，一共有多少糖？

假設小朋友每人分到 n 塊糖，總共有 N 塊糖，則
奶奶分得 (N-1)/3，
小弟弟分得 [2(N-1)/3 – 1]/3 = (2N-5)/9
爸媽分得  [2(2N-5)/9 – 1]/3 = (4N-19)/27
3位小朋友 2(4N-19)/27 – 1 = 3n
==> 8N=65+81n ==> n=7，and N=79. [因 n 及 N 是正整數]
答案是總共有 79 塊糖。

[信堅註: 求 8N=65+81n 之解答的方法如下: 先將此方程式改寫成
N = 8+10n + (1+n)/8, 則知 n=7+8a 都是可能的解答
==> N = 79 + 81a 都是可能的解答 (a 是正整數)
此題限制 N < 100, 因此解答是 a=0, N=79. 如果將題目改為 N 稍小於 500，則答案是 a = 5, N = 484.]

【問題19】兩支臘燭
粗蠟燭和細蠟燭長短一樣。粗蠟燭可以點５小時，細蠟燭可以點四小時，同時點燃這兩支蠟燭，點燃一段時間後，粗蠟燭是細蠟燭的４倍。您能夠算出這兩隻蠟燭兩支蠟燭點了多少時間嗎？ 
4(1-x) = 5(1-4x) => x=1/16 4x (1-1/16) = 15/4 hr. (x 是剩餘長度)

改成比較容易: 粗蠟燭和細蠟燭長短一樣。粗蠟燭可以點6小時，細蠟燭可以點4小時，同時點燃這兩支蠟燭，點燃一段時間後，粗蠟燭是細蠟燭的2倍。您能夠算出這兩隻蠟燭兩支蠟燭點了多少時間嗎？
T = 4(1-x) = 6(1-2x) => x=1/4 T = 4 x (1- ¼) = 3 hr.
剩餘長度: 粗蠟燭= 1-T/6 細蠟燭= 1-T/4
點的時間     0      1       2        3
粗蠟燭         1    5/6     2/3    1/2
細蠟燭         1    3/4     1/2    1/4
倍數             1    9/10   4/3     2

【問題20】菲波拉契系列 (Fibonacci Sequence)
十三世紀初，義大利出版了本研究算術和代數的書籍<<算盤書>>，它是當時歐洲人推廣阿拉伯數字的重要書籍。數學家菲波拉契在書中提出一個樂趣的題目：「假設一對兔子配成對偶後，在第二個月後，便可每月生下一對 (一雌一雄) 的小兔子。假設每隻兔子都能健康存活。問: 如果開始有一對初生兔子，一年之後，總共會有多少對兔子呢？」

列表計算:
幾月後               1  2  3  4  5  6   7   8    9   10   11   12    13
數量 (生產期)    0  0  1  1  2  3   5   8   13   21   34   55   89
(出生兩個月內)  0  1  0  1  1  2   3   5    8   13   21   34    55
(出生一個月內)  1  0  1  1  2  3   5   8  13    21  34   55    89
總數                   1  1  2  3  5  8 13 21  34    55  89 144  233

如此下去，每個月兔子的成對個數分別是1，1，2，3，5，8，13，21，34, 55, 89, 144, 233, …….。這數列我們稱之為斐波拉契系列，且其特徵是在每個數字是前兩個數字的總和。

如以數學術語表達，斐波納契數的序列 F_n 的遞歸關係是：
F_n=F_n-1+_Fn-2,  n >3,  F₁=1, F₂=1.

【問題21】喝汽水問題
有n 瓶汽水，每兩個空瓶可換一瓶汽水，每三個瓶蓋可換瓶汽水，問: 總共可喝幾瓶汽水? 答案是 N=6n-7, 剩一瓶蓋及二空瓶。
(若借貸7空瓶及7 瓶蓋，則可多喝7瓶, 即 N = 6n)

列表解題
汽水    空瓶    瓶蓋
2           2         2
1+0      0+1     2+1
0+1      1+1     0+1
1+0      0+1     1+1
__________________
5            1          2
==> n=2，總共可喝 5=6xn-7瓶汽水, 剩一空瓶及二瓶蓋。

汽水       空瓶      瓶蓋
3              3            3
1+1        1+2        0+2
1+0        1+1        2+1
1+1        0+2        0+2
1+0        0+1        2+1
0+1        1+1        0+1
1+0        0+1        1+1
___________________
11           1             2
==> n=3，總共可喝 11=6xn -7 瓶汽水, 剩一空瓶及二瓶蓋。
1           1+1         2+1  若再增加一瓶汽水
1+1       0+2         0+2
1+0       0+1         2+1
0+1       1+1         0+1
1+0       0+1         1=1
___________________
17           1             2
==> n=4， 總共可喝 17= 6xn -7 瓶汽水, 剩一空瓶及二瓶蓋。

==> 一般公式是若有n瓶汽水，則總共可喝 N = 6n-7 瓶汽水, 剩一空瓶及二瓶蓋。此地的 -7 是所謂量子化糾正 (quantization correction)，因空瓶與瓶蓋是整數，不可細分。

若向銀行借 7 空瓶及 7瓶蓋 [量子力學的述語叫真空波動 (vacuum fluctuation)]，則
6n-7        1          2
          -7+7+1   -7+7+2
4+3       -7+7       -7+7
___________________________
6n           0             0
==> 一般公式是，若有n瓶汽水，則總共可喝 N = 6n 瓶汽水, 沒剩下空瓶或瓶蓋。